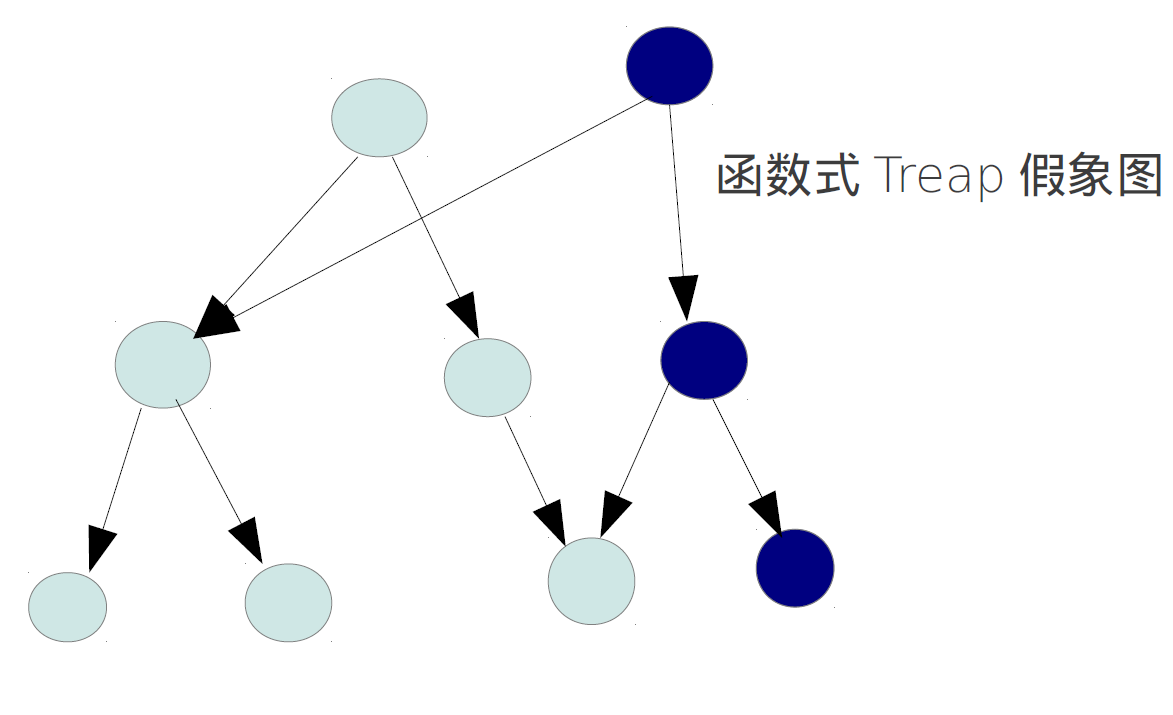
左偏树真是个超好写的东西!支持合并,插入,删除最小值三个操作。后两个操作都可以看成第一个操作的拓展,如删除最小值是合并根的两棵子树,插入则直接将元素看作一个左偏树——所以只要写个Merge就可以了!
左偏树保证左子树深度大于等于右子树深度,同时符合堆性质。合并LT1,LT2(假设LT1中最小值比LT2小,否则交换)时,递归合并LT1的右子树和LT2替换掉LT1,然后如果LT1不符合左偏性质,则交换LT1的子树。
小小的提示:构树时,逐个插入是O(nlgn)的。这里可以有O(n)的复杂度的算法:先把所有元素构成n个单元素左偏树放进队列,然后每次取出两个合并后放入队列尾,直到只剩下一棵左偏树。
——http://seter.is-programmer.com/posts/30733.html
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
#include<iostream> #include<cstdio> #include<algorithm> #include<vector> #include<cmath> #include<cstring> #include<queue> #define S(x) T[(x)].s #define L(x) T[(x)].s[0] #define Ln(x) T[T[(x)].s[0]] #define R(x) T[(x)].s[1] #define Rn(x) T[T[(x)].s[1]] #define F(x) T[(x)].f #define W(x) T[(x)].w #define Z(x) T[(x)].size #define D(x) T[(x)].depth #define PB(x) push_back(x) #define PS(x) push(x) #define MP(x,y) make_pair(x,y) using namespace std; typedef long long LL; const int MAXN=100; const int INF=2147483647; const int NINF=-1<<30; const int ERR=-1; bool getint(int &x){ x=0;int n=1; char c=getchar(); while(((c-'0')>=10)||((c-'0')<0)){n=1;if(c=='-')n=-1;c=getchar();if((int)c==-1)return false;} while(((c-'0')<10)&&((c-'0')>=0)){x=x*10+(c-'0');c=getchar();}x*=n; return true; } void priint(int k){ if(!k)putchar('0'); int t=0;char ch[30]; while(k>0)ch[++t]=k%10,k/= 10; while(t)putchar(ch[t--]+'0'); putchar(10); } struct Node{int s[2];int w;int depth;Node():w(0),depth(0){s[0]=s[1]=0;}}; Node T[MAXN]; int Merge(int a,int b){ if(!(a&&b))return a|b; if(W(a)>W(b))swap(a,b); R(a)=Merge(R(a),b); if((!L(a))||D(L(a))<D(R(a)))swap(R(a),L(a)); D(a)=L(a)?D(L(a))+1:0; return a; } int sz,root,a,b; int main(){ D(0)=-1; int x; while(getint(x)){ if(!x)getint(W(++sz)),root=Merge(root,sz); else priint(W(root)),root=Merge(L(root),R(root)); } return 0; } |