偶然间翻PDF时看到了FHQ神犇的WC论文……看了一遍没记住什么……除了函数式编程其他也……就那样吧……顺手把CLJ的论文也看了一遍……//可持久化做法很多,函数式是种比较科学的实现……暴力复制、wzk树什么的就不说了……
然后函数式编程早就接触过但从来没有研究过TAT显然函数式线段树最成功的应用(之一?)就是主席树了……
函数式编程
修改元素是数据结构的一个基本操作,平常的实践中我们比较常见的就是直接改储存的值,而函数式编程中,我们从不去修改值,而是再定义一个。
对应在线段树操作中,我们每次修改值,都不会去修改任何节点,而是返回一棵新的树。
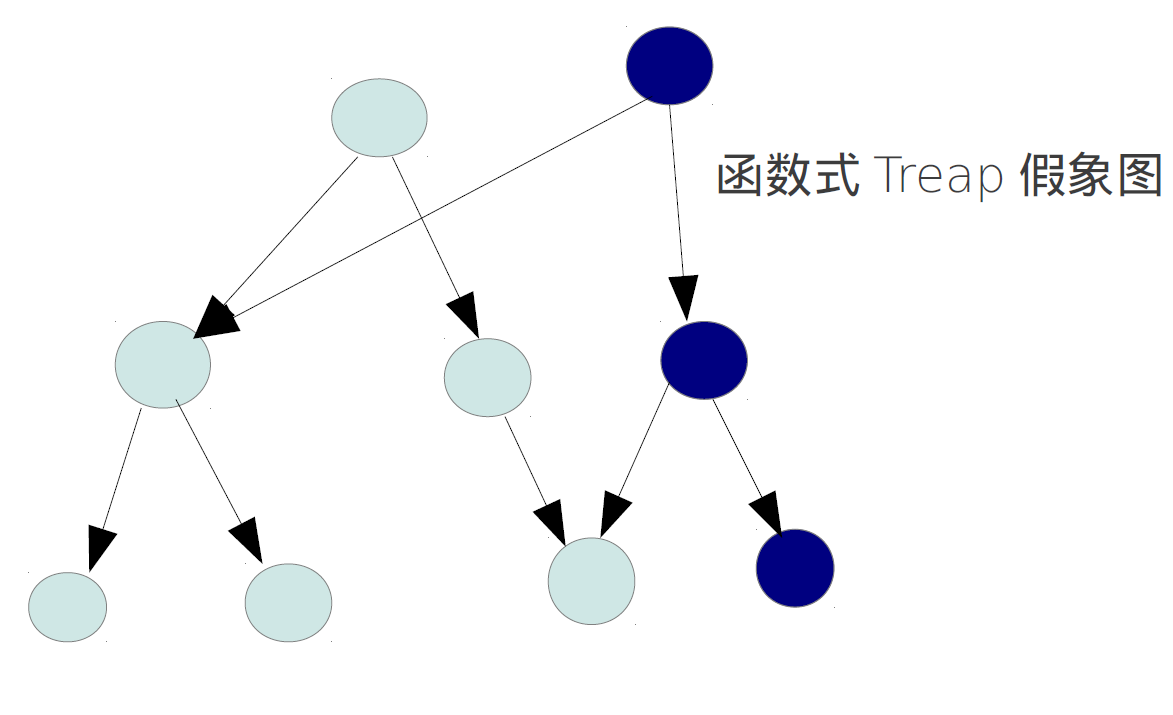
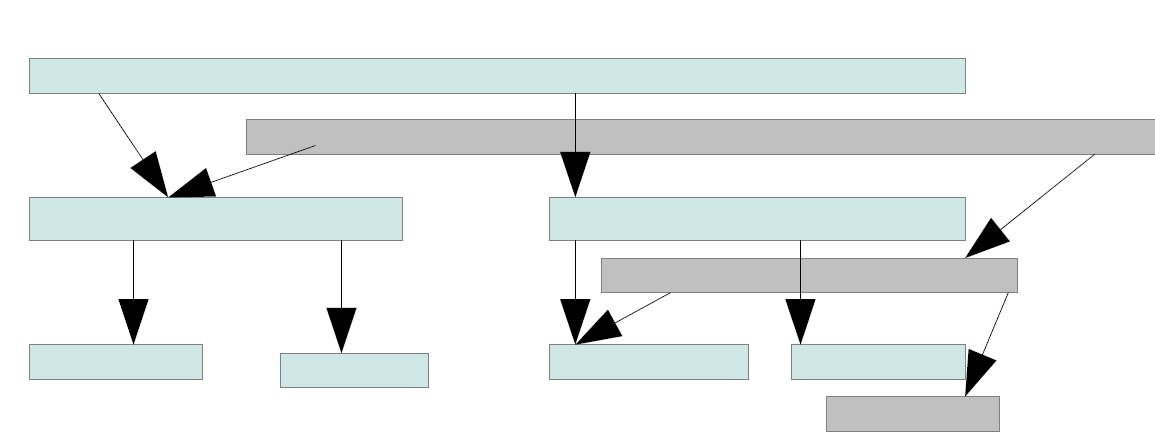
图片来自范
因为保证所有节点都不会被修改,所以我们可以重用未受影响的节点。显然,函数式线段树中,插入操作的时间、空间复杂度都是O(log n),其他操作与正常线段树无异。
主席树
主席树是一种利用函数式线段树维护数列的数据结构,一般用来解决区间第K大数问题。设数列长度为NN,数据范围为n,已离散化。
不支持修改的主席树(前缀和主席树)
……不支持修改的主席树在我的笔记中记为前缀和主席树…自己取的名字。。。
前缀和主席树由N棵线段树组成,第i棵Ti是对于[1,i]建一棵以序列里的值为下标,储存区间里出现该值的次数的线段树,也可以看作是Ti-1插入a[i]后的线段树。
注意到所有的树是同构(?)的,Ts-1和Tt可以直接相减得到T[s,t],在树上进行二分就可以得到区间K大值。
当然,所有的线段树都指函数式线段树。
代码:Via http://www.cnblogs.com/Rlemon/archive/2013/05/23/3094635.html 我自己码的实现惨不忍睹…这是和我的风格最接近的一个…以下是按我的笔记格式码的…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
#define w(i) T[(i)].w #define ls(i) T[(i)].ls #define rs(i) T[(i)].rs using namespace std; const int MAXNN; struct node{ int ls,rs,w; node(){ls=rs=w=0;} }T[MAXNN*20]; int a[MAXNN],root[MAXNN],sz,m; void ins(int &i,int l,int r,int x){ T[++sz]=T[i]; i=sz; w(i)++; if (l==r) return; int m=(l+r)>>1; if (x<=m) ins(ls(i),l,m,x); else ins(rs(i),m+1,r,x); } int query(int i,int j,int l,int r,int k){ if (l==r) return l; int t=w(ls(j))-w(ls(i)); int m=(l+r)>>1; if (t>=k) return query(ls(i),ls(j),l,m,k); else return query(rs(i),rs(j),m+1,r,k-t); } int main(){ //DO YOLO root[0]=0; sz=0; for (int i=1;i<=N;i++){ root[i]=root[i-1]; ins(root[i],1,n,a[i]); } //支持操作: //QUERY(s,t,k):query(root[s-1],root[T],1,n,k); return 0; } |
支持修改的主席树(树状主席树)
还记得当年学数据结构时如何维护带修改区间[s,t]的区间和吗?
树状数组,简单高效。既然我们维护的是一个线段树的前缀和,何不用树状数组维护呢?
脑补一棵树状数组,每个节点是一棵线段树 。修改时,我们仅需修改log n棵线段树即可。
//貌似只有我叫它树状主席树……正解是树状数组套主席树。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
#define ls(i) T[i].ls #define rs(i) T[i].rs #define w(i) T[i].w using namespace std; const int MAXNN; struct node{ int ls,rs,w; node(){ls=rs=w=0;} }T[MAXNN*20]; vector<int> Ql,Qr; int n,m,sz,NN; int a[MAXNN],root[MAXNN],rooto[MAXNN]; inline int lowbit(int x){ return x&-x; } void build(int &i,int l,int r,int x){ T[++sz]=T[i]; i=sz; w(i)++; if (l==r) return; int m=(l+r)>>1; if (x<=m) build(ls(i),l,m,x); else build(rs(i),m+1,r,x); } void ins(int &i,int l,int r,int x,int v){ if (i==0){ T[++sz]=T[i]; i=sz; } w(i)+=v; if (l==r) return; int m=(l+r)>>1; if (x<=m) ins(ls(i),l,m,x,v); else ins(rs(i),m+1,r,x,v); } void BITins(int pos,int x,int v){ for (int i=pos;i<=NN;i+=lowbit(i)){ ins(root[i],1,n,x,v); } } int STquery(vector<int> Q1,vector<int> Q2,int l,int r,int k){ if (l==r) return l; int c=0; int m=(l+r)>>1; //查询[l,m] for (int i=0;i<Q1.size();i++) c-=w(ls(Q1[i])); for (int i=0;i<Q2.size();i++) c+=w(ls(Q2[i])); //线段树上二分 for (int i=0;i<Q1.size();i++) Q1[i]=(c>=k?ls(Q1[i]):rs(Q1[i])); for (int i=0;i<Q2.size();i++) Q2[i]=(c>=k?ls(Q2[i]):rs(Q2[i])); if (c>=k) return STquery(Q1,Q2,l,m,k); else return STquery(Q1,Q2,m+1,r,k-c); } int query(int l,int r,int k){ Ql.clear();Qr.clear(); //原始数组 Ql.push_back(rooto[l-1]); Qr.push_back(rooto[r]); //操作数,用树状数组维护 for (int i=l-1;i>0;i-=lowbit(i)) Ql.push_back(root[i]); for (int i=r;i>0;i-=lowbit(i)) Qr.push_back(root[i]); return STquery(Ql,Qr,1,n,k); } int main(){ //DO YOLO sz=0; memset(rooto,0,sizeof(rooto)); memset(root,0,sizeof(root)); for (int i=1;i<=n;i++){ rooto[i]=rooto[i-1]; build(rooto[i],1,n,a[i]); } //支持操作: //UPDATE(x,v):[ // BITins(x,a[x],-1); // BITins(x,v,1); // a[x]=v; //] //QUERY(s,t,k):[ // query(s,t,k); //] } |
临时建立节点的主席树
//待补完
参见clj的wc论文