神犇说世上的美有三种，一是优美精致的数据结构，二是巧夺天工的神奇算法，三是你温暖世界的笑容

计算机之所以叫做计算机，就是因为它在“计算”这一件事上做的可以比人类快。而我们的任务，就是告诉计算机要如何去进行一个计算，也就是要实现一个算法。
想要让程序更快，除了要提升计算机处理器的运行速度之外，最重要的就是要提升算法的效率，以及算法的在这个计算机上实现的的速度。
做同样的一件事情，可以有无数种做法。比如说给一些数字排序，就有好几种做法。那么要怎么比较他们的速度呢？
最直观的做法自然是写出对应的程序，给定一个输入，然后比较一下他们的运行时间。这样的做法简单粗暴，然而并不能给我们关于这些算法的更多信息，也只能反映这些算法在这个特定输入的情况，误差也不容小视。
更为严谨的做法，是对这个算法进行数学上的分析，以得出这个算法在理论上的运行效率。
以选择排序为栗子把
（然后把栗子剥开吃掉~

来看看他的运行原理

第零轮从所有的n个数据中找出最小的，需要对每个\(j\in \left ( 0,n \right )\)进行一次比较，共n-1次
第一轮从剩下的n-1个数据中找出最小的，需要对\(j\in \left ( 1,n \right )\)每个进行一次比较，共n-2次
……
第i轮从剩下的n-i个数据中找出最小的，需要对\(j\in \left ( i,n \right )\)每个进行一次比较，共n-i-1次
第n-2轮从剩下的2个数据中找出最小的，需要进行一次比较

总共需要进行 \(\sum_{k = 1}^{n-1} k=\frac{n\left ( n-1 \right )}{2}\)次比较
然后每轮需要对数据进行一次交换，合计是\(\left ( n-1 \right )\)次交换
也就是说，这个程序所需要运行的时间大致上是
\(T=\frac{n\left ( n-1 \right )}{2}T_{0}+\left ( n-1 \right )T_{1}\)，其中\(T_{0}\)为一次比较需要的时间，\(T_{1}\)为一次交换所需要的时间
当n很大的时候，对T的量级起到决定性作用的将会是什么呢？
（还记得函数在无穷大的极限吗？
n趋向于无穷大时，起作用的将会是n的二次项，也就是\(\frac{n^{2}}{2}T_{0}\)
那么可以看出，选择排序的算法的运行时间在n充分大的时候，大致正比于\(n^{2}\)

再来看一看冒泡排序

显然，冒泡排序也是需要对整个数据进行\(\sum_{k = 1}^{n-1} k=\frac{ n\left ( n-1 \right )}{2}\)次比较。
而需要执行的交换次数呢，就相对不好分析了，但是显然是小于比较的次数的。
（详细的说，是数据中逆序对的个数
那么冒泡排序的运行时间在n充分大的时候，也是大致正比于\(n^2\)的。
而且这两个排序的速度的量级，和所给定的输入无关，最好、一般和最坏的情况下，都是\(n^2\)。
冒泡排序还有一种常见的优化

也就是说，如果一次循环中没有发生过交换，那么肯定这个序列已经排好序了（为什么？）。
那么给它一个已经排好序的序列，就只需要n-1次判断就可以发现数据已经排好序了。
即bubble_sort2最好的情况下，当n充分大时，速度正比于n，一般和最坏情况下都是正比于n^2
）每次都得带上当n充分大时……正比于……实在是累死我了
还好数学家们也发现了这个问题，所以说对于这种运行时间的表述，采用了一种记号系统：渐进记号
定义如下
给定两正值函数f和g,定义:
\(f(n)=O(g(n))\),当存在正实数\(c\)和\(N\),使得对于所有的\(n \geq N\),有\( |f(n)| \leq |cg(n)| \)

这样的话，我们就可以说，冒泡排序和选择排序的运行时间是\(O(n^2)\)的
显然，按照定义，它们也是\(O(n^3)\)的，\(O(n^4)\)的…大O记号表示的是一个相对的关系，可能并不一定是精确的
还有一种对称的关系：
\(f(n)=\Omega(g(n))\),当存在正实数\(c\)和\(N\),使得对于所有的\(n \geq N\),有\( |f(n)|\geq |c g(n)| \)
这样，我们就可以说bubble_sort2的运行时间是\(\Omega(n)\)的，因为在最好情况下它也至少需要\(n\)次比较
如果\(f(n)=\Omega(g(n))\)且\(f(n)=O(g(n))\)，那么我们可以说\(f(n)=\Theta(g(n))\)
\(O\)、\(\Omega\)、\(\Theta\)的关系就像“小于等于”、“大于等于”和“等于”一样
当然，还有\(o\)、\(\omega \)这两个记号，是用来表征“小于”、“大于”的关系的。
\(f(n)=o(g(n))\),当对于所有的正实数\(c\)，存在正实数\(N\),使得对于所有的\(n \geq N\),有\(|f(n)|<|c g(n)|\) \(f(n)=\omega(g(n))\),当对于所有的正实数\(c\)，存在正实数\(N\),使得对于所有的\(n \geq N\),有\(|f(n)|>|c g(n)|\)
在实际使用中，在不引起歧义的情况下为了书写方便，一般上常用大O记号，也就是\(O(f(n))\)的表示方法来表示算法的复杂度。
很多场合常用\(O(f(n))\)来表示\(\Theta(f(n))\)的意义，接下来基本上也会采用这样的记法。

黄炜老师的补充
一般情况下，算法中基本操作重复执行的次数是问题规模 n 的某个函数 f(n) 算法的时间度量记作 T(n) = O(f(n))，他表示随着问题规模n增大，算法执行时间的增长率和 f(n) 的增长率相同，乘坐算法的渐进时间复杂度（Asymptotic Time Complexity），简称时间复杂度。
算法时间复杂度从小到大依次是： O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) <O(nn)
时间复杂度越高，算法消耗cpu就越高，执行速度就越慢。
分析时间复杂度代码举例如下:

C

int sum = 1, n = 100; //O(1): sum = (1 + n) * n / 2;

1 2 3

int sum = 1, n = 100; //O(1): sum = (1 + n) * n / 2;

这是一次性完成，n不影响sum的计算时间，多大的n也是很快搞定。

C

//O(logn): while((sum < n){ sum = sum * 2; }

1 2 3 4

//O(logn): while((sum < n){     sum = sum * 2; }

循环的次数是随着你增长而增长的，其速度并不如n，而是和n的对数差不多。

C

//O(n): for(int i=0; i<n; i++){ sum += n; }

1 2 3 4

//O(n): for(int i=0; i<n; i++){     sum += n; }

这会计算耗时的增长速度就和n一样了

C

//O(n^2): for(int i = 0; i < n; i++){ for(int j = 0; j < n; j++){ sum += 1; } }

1 2 3 4 5 6

//O(n^2): for(int i = 0; i < n;  i++){     for(int j = 0; j < n;  j++){         sum += 1;     } }

虽然和之前结果一样，但是多了好几步。。而且计算规模是平方的关系

C

//O(n^2): for(int i = 0; i < n; i++){ for(int j = i; j < n; j++){ sum += 1; } }

1 2 3 4 5 6

//O(n^2): for(int i = 0; i < n;  i++){     for(int j = i; j < n;  j++){         sum += 1;     } }

这个也是n平方，当然了确切说是n平方的一半，但我们主要讲增长速度的级别，系数并没有差别

现在回头来看一看刚才的几个算法
selection_sort最好、平均和最坏情况都是\(O(n^2)\)
bubble_sort1最好、平均和最坏情况也都是\(O(n^2)\)
bubble_sort2最好情况是\(O(n)\),平均和最坏情况是\(O(n^2)\)
从bubble_sort1和bubble_sort2的复杂度的比较就会发现一些情况下bubble_sort2更快，而一般情形和最坏情况速度的量级相当。
有没有更快的方法呢？
有的

这个是归并排序，基本的思路如下：
\(n=1\)时，什么都不做
\(n=2\)时，排序这两个数
如果\(n\gt 2\),把需要排序的数列等分成两半，分别进行归并排序，
之后把两个排序好的数列进行归并，也就是依次选择当前两个排好序的数列的第一个中大（小）者加入归并的数列，直到两个数列都归并完成
就是酱紫~

那要怎么分析他的运行时间呢？
设它的运行时间为\(T(n)\)好了
根据算法的定义我们有
\(T(n)=2*T(\frac{n}{2})+O(n)\)
\(T(1)=O(1)\)
我们可以用数学归纳法来证明\(T(n)=O(n \log_{2}n )\)，就是用\(T(\frac{n}{2}) \leq c \frac{n}{2} \log_{2}(\frac{n}{2})\)推出\(T(n)=O(n \log_{2}n)\)，这个证明留作练习（雾
对于这样的递归式，有一套方法来求解它，有兴趣可以看一看
所以说…归并排序的运行时间是\(O(n \log_{2}n)\)
显然\(O(n \log_{2}n)=o(n^2)\)（复习一下刚才渐进记号的定义吧），那么归并排序比selection_sort和bubble_sort1快，比bubble_sort2的最好情况慢。
还有没有更快的呢？
有一种排序叫做快速排序。

原理长这样：
从数列中挑出一个元素，称为"基准"（pivot），
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面。
分别把小于基准值元素的子数列和大于等于基准值元素的子数列排序。
举个例子：(每次展开一层递归，始终选取最后一个作为基准，以[]表示)
8 7 3 1 5 6 2 4
(3 1 2) [4] (8 7 5 6)
(1 [2] 3) [4] (5 [6] (8 7))
(1 [2] 3) [4] (5 [6] ([7] 8))

看一看动图：

都说是快速排序，那么它到底有多快呢？
大家可以猜一猜
答案是：最坏情况是\(O(n^2)\)，也就是说不好的时候和冒泡、选择排序一样慢。
然而它有一个\(O(n \log_{2}n)\)的最好和平均情况，和归并排序相同。
让我们来看看这两个是怎么算出来的：
一般情况下，如果数组被划分成\(i\)和\(n-i\)两部分，那么有
\(T_{c}(n)=T(i)+T(n-i)+O(n)\)
最糟糕的时候，数组被划分成1和n-1两部分，有
\(T_{w}(n)=T(1)+T(n-1)+O(n)\)
解得
\(T_{c}(n)=O(n \log_{2}n)\)
\(T_{w}(n)=O(n^2)\)
快速排序的麻烦主要是出在基准的选择上，如果选择的基准不巧的话，就会出现这种非常不平衡的情况。
比如说对123456789排序（事实上已经排好了，倒序的时候也一样），每次都选择最后一个数为基准，那么第一次划分就成了
(1 2 3 4 5 6 7 8) [9]
第二次
((1 2 3 4 5 6 7) [8]) [9]
……每次只能选出一个，这不是变成了选择排序了吗？
所以说，枢纽元的选择会极大的影响快排的效率。
为了避免这种情况，一般上会采取一些措施，比如说随机选取一个基准值，或者是选三个数取其中位数，或者是先把待排序的数组完全打乱（好暴力然而效果拔群），这样的做法都可以一定程度上避免快排退化。
既然快排和归并都是\(O(n \log_{2}n)\)的平均，而快排还有可能退化到\(O(n^2)\)，那为什么快排还是快排呢？
常数，常数，常数。
都是\(O(n \log_{2}n)\)，\(100*n \log_{2}n\)和\(0.01*n \log_{2}n\)显然差距还是蛮大的，渐进分析只能比较在n增长的过程中，两个算法运行时间之比的情况。
如果快排的最高次的系数是\(\frac{1}{2}\)，而归并排序的系数是1，那么\(n\)充分大的时候平均状况下快排会比归并快一倍。
这个时候，归并又比冒泡和选择排序快了\(\Theta ( \frac{n}{\log_{2}n})\)。
显然随机数据量大的时候，归并和快排相对于冒泡和选择的优势会越来越大，快排又借常数小更胜一筹。而且快速排序可以省去很多内存（空间复杂度）
）FYI：快排为什么会那么快？（堆排序也是一种\(O(n \log_{2}n)\)的基于比较的排序）

插入排序是选择未排序数列的第一个数，插入到已排序数列的合适位置。一定的优化以后，如果数列是基本排序的，那么插入排序的最好时间可以到\(O(n)\)

STL里面就采用了插入排序作为快排的补充优化。
重点是，如果数列是基本排序的，那么插入排序的最好时间可以到\(O(n)\)
希尔排序就是基于这个特性而开发的。它将原始序列按照不同的步长分组，分别进行插入排序，重复多次，直到最后对整个序列进行一次插入排序。
摘录维基百科的介绍
例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了，然后再以3为步长进行排序：

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
排序之后变为：

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94
最后以1步长进行排序（此时就是简单的插入排序了）。

这个”不同的步长“就大有文章了。Donald Shell也就是希尔排序的发明人用的是步长n/2并且对步长取半直到步长达到1，然而事实证明这个并不算好用。
然后看看这些丧心病狂的步长吧。


除了常数，还有一些因素会影响到算法的运行时间：
1.低阶项的常数大小。虽然n趋向于无穷大的时候低阶项可以忽略，但是在实际的程序应用中，我们面对的题目都是有界的。
这个时候，就要具体地考虑一下低阶项会不会显著影响到程序的时间。在上面的例子中，我提到了选择排序的\(T=\frac{n\left ( n-1 \right )}{2}T_{0}+\left ( n-1 \right )T_{1}\)
假如说\(T_1 \gg T_2\)且\(\frac{T_1}{T_2}\gg n\)的时候，\(T_1 n\)反而是决定性的因素
（比如说要排序的是刻在石板上的字,你需要把它凿掉再刻上去?）
2.递归的边界条件
快速排序在大规模的随机数据表现良好，然而到了小规模就不给力了。所以说有些实现，就会在数据小的时候选用插入排序来作为递归的边界，而不是快排到只剩1~2个数。
还有一个内省排序IntroSort，就是一个快排丧心病狂的魔改：
1.一般情况下用快排
2.如果发现快排划分不好的话改用堆排
3.如果需要排序的数小于16个，则不进行排序
4.以上过程结束后，再来一次插入排序（为什么是插入排序？）
详见STL sort源码剖析

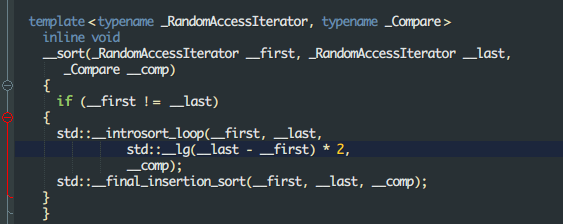
这样便通过规避快速排序在小数据偏慢的问题加快了排序的速度，也避免了快排退化到\(O(n^2)\)的情况

[时间复杂度 Time Complexity of Algorithms by Liqueur Librazy is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available at SoWhat ACM转载协议.